[자료구조] 세그먼트 트리

세그먼트 트리에 대해 알아봅시다. 세그먼트 트리란 구간의 합을 리프 노드에 저장하는 자료구조로 O(logN) 시간 복잡도를 가지고 연결된 데이터의 구간합을 구할 수 있습니다.

 

데이터 : 4 9 3 8 6 9 7 9 7 9 2 3 4 8 7 가 주어 질 때 구간의 합을 구하는 방법은 다음과 같습니다.

 

가장 단순하게 선형적으로 구하는 방법으로 시간 복잡도 O(n)가 나올 것입니다. 좀 더 개선하면 누적 합과 같이 각 행을 처음부터 해당 칸의 합을 저장해서 O(n) 이후 O(1)으로 계산할 수 있습니다.

 

누적합

4 13 16 24 30 39 46 55 62 71 73 76 80 88 95와 같이 저장될 것이며 O(n) 이 걸립니다. 이후 3번째부터 12번째 데이터 합은 인덱스 12번째 인덱스 - (3-1)번째 인덱스로 구할 수 있을 것입니다.

 

이때 세그먼트 트리를 사용하면 O(logN)번으로 구간 합을 구할 수 있습니다.

 

세그먼트 트리는 완전 이진트리로 구현되며 배열을 사용해서 구현할 수 있습니다. 그렇기 때문에 데이터 개수가 필요합니다. 그렇다면 어떻게 배열로 구현이 가능한지 알아봅시다.

 

8개의 데이터가 주어질 때 트리는 다음과 같을 것입니다. 트리를 보면 부모 노드와 자식 노드에 보면 규칙이 있습니다.

부모노드가 n번째 데이터일 때 자식 노드는 데이터의 2n번째와 2n+1번째라는 것을 알 수 있습니다. 이때 배열의 크기는 2**트리의 깊이 임을 알 수 있습니다. 데이터 크기 n이 주어졌을 때 트리의 깊이는 logN/log2의 반올림해서 깊이를 구할 수 있습니다. 예시 n = 15 일때 log15/log2는 3.xxx로 트리의 깊이는 4가 됩니다.

 

이제 배열을 활용 해서 세그먼트 트리를 구현해봅시다. 데이터를 가지고 있을 데이터와 구간의 합을 저장할 두 개의 배열이 필요합니다. 원본 데이터로 구간의 합을 저장하는 배열에 값을 저장해주고 원하는 구간의 합을 찾아 탐색하는 메커니즘입니다.

 

구간 합이 저장 될 배열에 값은 다음과 같을 것입니다.

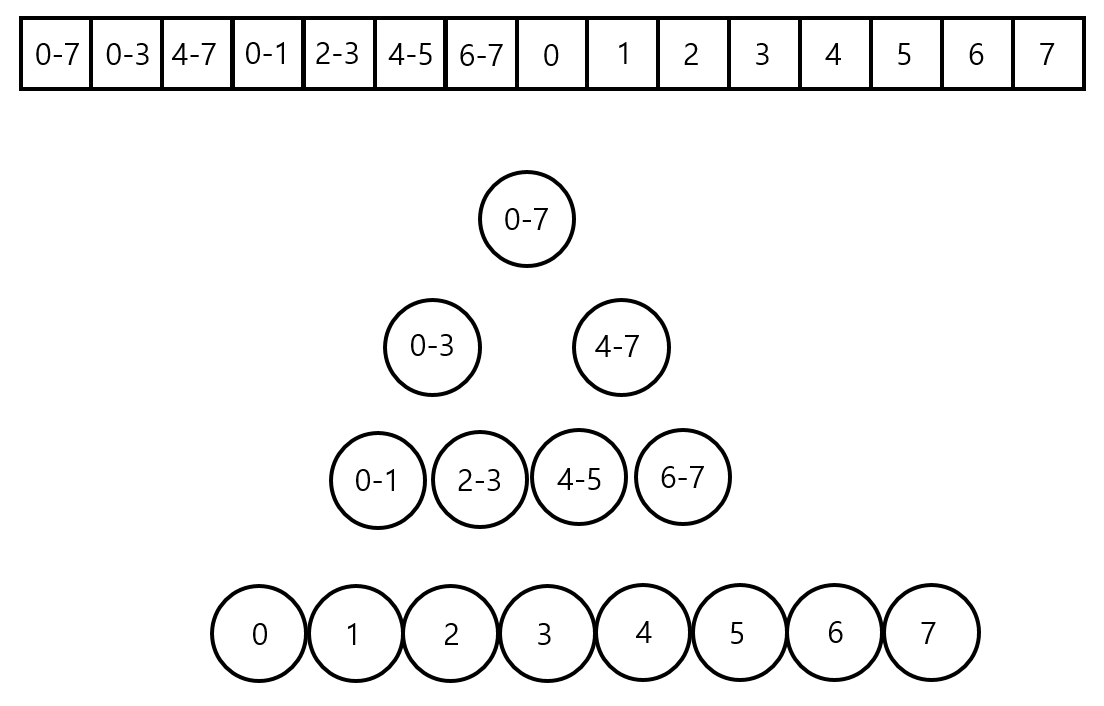
위의 배열이 아래 트리와 같은 의미를 가진다고 생각할 수 있습니다. 이때 2-5 사이 구간 합을 구하면 다음과 같을 것입니다.

 

2-5 구간이 루트부터 타고 내려가면서 2-5 구간에 분산된 노드를 찾아 더하게 됩니다. 동작 과정은 다음과 같을 것입니다.

구현해 봅시다.

static int n; // 데이터 사이즈
static long[] a,tree; // a 원본 데이터 tree 구간의 합이 저장

// tree 배열에 구간 합 넣기
private static void init(long[] a, long[] tree, int node, int start, int end) {
    if(start == end) tree[node] = a[start];
    else {
        init(a,tree,node*2,start,(start+end)/2);
        init(a,tree,node*2+1,(start+end)/2+1,end);
        tree[node] = tree[node*2]+tree[node*2+1];
    }
}

// a 배열이 변경되면 tree도 변하는 작업
private static void update(long[] a, long[] tree, int node, int start, int end, int index, long value) {
    if(index < start||index > end)return;
    if(start == end) {
        a[index] = value;
        tree[node] = value;
        return;
    }
    update(a,tree,node*2,start,(start+end)/2,index,value);
    update(a,tree,node*2+1,(start+end)/2+1,end,index,value);
    tree[node] = tree[node*2]+tree[node*2+1];

}

// 구간 합 찾기
private static long quary(long[] a, long[] tree, int node, int start, int end, int left, long right) {
    if(right < start || left > end)return 0;
    if(left <= start && end <= right) return tree[node];
    long l = quary(a, tree, node*2, start, (start+end)/2, left, right);
    long r = quary(a, tree, node*2+1,(start+end)/2+1,end, left, right);
    return l+r;
}

n = 15 일 때

a : [4, 9, 3, 8, 6, 9, 7, 9, 7, 9, 2, 3, 4, 8, 7]
tree : [0, 95, 55, 40, 24, 31, 21, 19, 13, 11, 15, 16, 16, 5, 12, 7, 4, 9, 3, 8, 6, 9, 7, 9, 7, 9, 2, 3, 4, 8, 0, 0]

이와 같이 구현할 수 있습니다.